Korrelation bestimmen
| Zurück zum Inhaltsverzeichnis |
| 0 - Testverfahren Zusammenhang |
| 1 - Bivariate Korrelation |
| 2 - Multiple Regression |
Testverfahren
Zusammenh�nge zwischen Variablen lassen sich �ber verschiedene Verfahren untersuchen.
Die zu w�hlenden Verfahren sind abh�ngig von der Anzahl der Variablen und der Art der Fragestellung.
Auswahl nach Variablenanzahl
Wollen wir zwei Variablen miteinander in Beziehung setzen, kann die Bivariate-Korrelation gepr�ft werden,
oder die lineare Regression.
Bei mehr als zwei Variablen ben�tigen wir die Analyseverfahren Multiple Korrelation
oder Multiple Regression.
Auswahl nach Fragestellung
Handelt es sich bei der Fragestellung um eine ungerichtete Fragestellung, nutzen wir Korrelationen.
In diesem Fall k�nnen wir nicht sagen, dass eine Variable von einer anderen abh�ngt.
Die Variablen sind gleichberechtigt.
Bei gerichteten Fragestellungen k�nnen wir Regressionstests machen.
In diesem Fall gibt es unabh�ngige Variablen und davon abh�ngige Variablen.
Ein simples Beispiel: Die Anzahl von 3 Punktw�rfen im Basketball ist die unabh�ngige Variable
Die Anzahl der erzielten Punkte ist die abh�ngige Variable.
Wir k�nnen einen positiven Zusammenhang erwarten, da nicht geworfene W�rfe definitiv keine Punkte bringen.
Zusammenhangsst�rke
Als Messergebnis einer Korrelation wird ein Korrelationskoeffizient ausgegeben.
Der Korrelationskoeffizient l�sst sich ggf. unterschiedlich interpretieren,
je nach Untersuchung oder Fachdisziplin.
Im Fall der Forschung an der Westf�lischen Wilhelms-Universit�t M�nster im Fach Sport, galt die Orientierung an einem Dreischritt, der sich an Psychologischen Interpretationsvorgaben orientierte. Ein Wert von 0,2 bis 0,29 bezeichnet eine schwache (positive) Korrelation. Ein Wert von 0,3 bis 0,5 bezeichnet eine mittlere Korrelation. Ein Wert �ber 0.5 bedeutet eine starke Korrelation. Der Zahlenbereich erstreckt sich von -1 bis 1. Negative Werte werden identisch kategorisiert. Ein Wert von -0,6 bezeichnet eine starke (negative) Korrelation.
Die Fernuni Hagen nennt auf der folgenden Webseite andere Werte:
fernuni-hagen.de
Weitere Informationen finden sich u.A. auf folgender Webseite:
univie.ac.at
Ein weiterer Wert der bei PSPP ausgegeben wird ist die Signifikanz der Korrelation. Diese gibt an, ob die Korrelation gesichert scheint, oder ob sie vielleicht zuf�llig ist. Signifikanzwerte werden (meist) in den folgenden Intervallen interpretiert: 0,05 bedeutet signifikant, 0,01 bedeutet hoch signifikant und 0,001 h�chst signifikant. Um so kleiner der Signifikanzwert ist, desto weniger zuf�llig sind die Ergebnisse.
Welche Zusammenh�nge kann Korrelation ausdr�cken?
Bei der Analyse von Zusammenh�ngen k�nnen verschiedene F�lle auftreten.
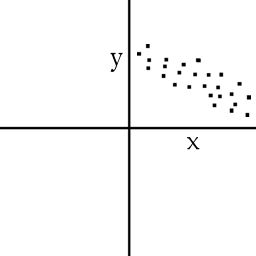
Ein Zusammenhang kann Linear negativ sein, der Wert des Korrelationskoeffizienten
liegt dann zwischen (ca.) -0,2 bis -1.
Wenn der Wert einer Variable X ansteigt, dann sinkt der Wert einer Variable Y.
Der Wert von Y steigt/sinkt umgekehrt vom Wert von X.
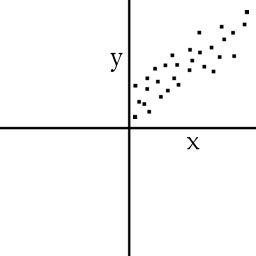
Zusammenh�nge k�nnen auch linear positiv sein, wenn der Wert der Variable X steigt, dann steigt auch der von Y an. Der Wert von Y steigt/sinkt mit dem Wert X.
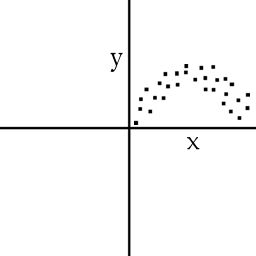
Ein weiterer Zusammenhang ist ein nichtlinearer Zusammenhang. Dieser Zusammenhang ist mit dem Korrelationstest nicht zuverl�ssig abbildbar. Wenn ihr in der grafischen Analyse eurer Daten seht, das die Verteilung z. B. gebogen ist, dann m�sst ihr dies unbedingt nennen. Ansonsten begeht ihr ggf. den Fehlschluss, dass es keinen Zusammenhang gibt - nur weil euch der Test Zahlenwerte angibt, die f�r keine Korrelation sprechen.
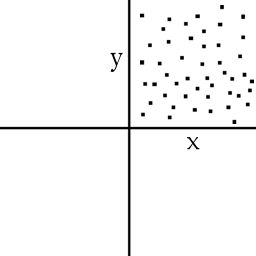
Und der letzte Fall der Zusammenhangsanalyse ist, dass kein Zusammenhang besteht.
Interpretationsfehler bei Korrelationen
Wichtig bei der Untersuchung von Zusammenh�ngen ist die korrekte, bescheidene, Interpretation der Ergebnisse.
Selbst wenn sich starke Korrelationen finden, d�rfen wir niemals einen kausalen Zusammenhang annehmen.
Korrelation sagt nur aus, dass zwei Variablen sich �hnlich zueinander entwickeln.
Als Beispiel f�r die Fehlerhaftigkeit einer Schlussfolgerung auf einen Kausalzusammenhang l�sst sich der Fehlschluss auf eine der gef�hrlichsten Sportarten Deutschlands nennen. Die sechsth�chste Todeszahl beim Sport hat welche Sportart? Kegeln. Kein Scherz. Eine Quelle findet sich hier: bisp-surf.de.
Kegeln ist also ein gef�hrlicher Sport? Eher nicht, hierbei handelt es sich um einen Fehlschluss aufgrund eines Zusammenhangs, ohne eine theoretische Grundlage f�r den Kausalzusammenhang zu haben. Zum Gl�ck sind wir Menschen anders als Statistikprogramme in der Lage, andere Gr�nde, bzw. unabh�ngige Variablen zu vermuten, die �ber die vor uns liegenden Variablen hinausgehen.
Die Personen beim Kegeln sterben vermutlich aufgrund einer anderen Variable, z. B. des Alters. Da eher �ltere Menschen Kegeln und da ein steigendes Alter nachweislich das Risiko zu sterben erh�ht, ist die Chance beim Kegeln zu sterben erh�ht.
Sinn und Anwendung von Korrelationen
Bei Korrelationen d�rfen wir keine Schlussfolgerungen auf den Kausalzusammenhang ziehen.
Wof�r sollen wir dann auf Korrelationen pr�fen?
Unsere Wissenschaftliche Arbeit begr�ndet sich auf theoretischen Grundlagen zu Wirkzusammenh�ngen.
Wir stellen aufgrund der Theorie Hypothesen auf.
Die Korrelationsanalyse dient als ein Pr�finstrument.
Wir k�nnen durch die Korrelationsanalyse aussagen, dass eine Hypothese durch die Korrelation gest�tzt
oder geschw�cht wird.
Falls ihr meint, dass sei zu wenig Aussagekraft, dann habt ihr die falsche Fragestellung gestellt ;) Denn wir pr�fen nur dann auf Korrelation, wenn wir eine ungerichtet Hypothese untersuchen wollen. Ungerichtete Hypothesen nutzen wir normalerweise dann, wenn wir nicht sicher sind, dass ein Zusammenhang besteht. Wir wollen damit vorsichtig schauen, ob da �berhaupt etwas ist. Wenn wir uns sicher sind, dann w�hlen wir hingegen eine gerichtete Hypothese, wo wir eine Variable als unabh�ngige Variable definieren und eine andere als abh�ngige Variable. Und bei gerichteten Hypothesen k�nnen wir die andere Analyseverfahren nutzen die mehr Aussagekraft haben, wie z. B. die Regression.
Nächste Seite: Bivariate Korrelation.
