Variablen automatisch berechnen
| Zurück zum Inhaltsverzeichnis |
| 0 - Summe berechnen |
| 1 - Logische Zusammenhänge prüfen |
Logische Zusammenhänge prüfen
Nach dem wir eine einfache mathematische Operation berechnet haben, können wir nun auch kompliziertere Zusammenhänge berechnen. Hier soll es jedoch um einen anderen Aspekt gehen. Wir können mittels logischer Zeichen Zusammenhänge prüfen.
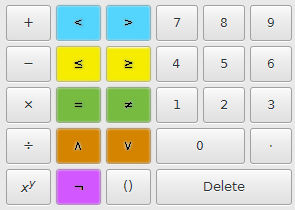
Blau markiert sind die Relationen von größer > und kleiner < . Gelb markiert sind die Relationen von größer oder gleich und kleiner oder gleich. Grün markiert sind die Relationen von gleich und ungleich. Orange markiert sind die logischen Konjunktionen Und ^ und Oder. Pink markiert ist die Negation Nicht.
Hinweis:
Die Zeichen auf den Schaltflächen sind nicht optisch identisch mit den Zeichen auf der Tastatur.
^ als logisches Und Zeichen wird mit & abgebildet.
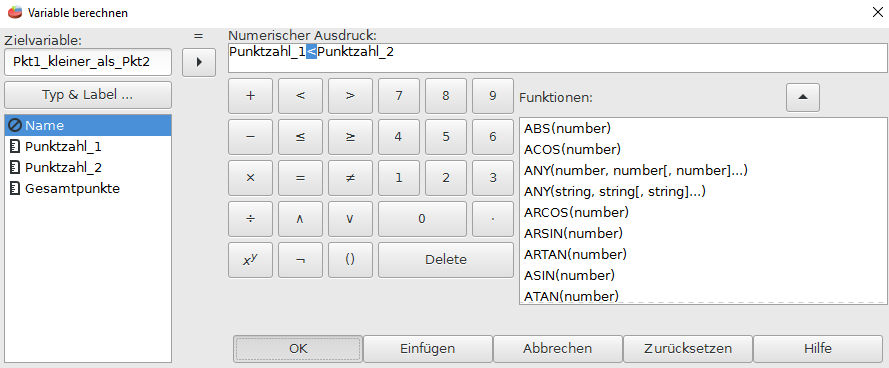
Mit den logischen Bausteinen können wir Zusammenhänge überprüfen. Im Beispiel wird geprüft, ob die Punktzahl 1 kleiner ist als die Punktzahl 2. Wir schreiben links unter Zielvariable hin, welche Variable überschrieben werden soll, bzw. welche Variable neu angelegt werden soll. Dann wählen wi die entsprechen Variablen als Basis (links unten) und fügen das logische Zeichen für kleiner < ein. Danach klicken wir auf OK.
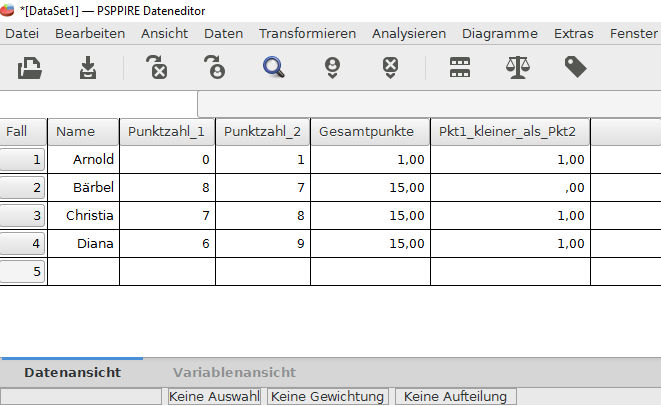
Im Bild unten sehen wir, das die Zielvariable Pkt1_kleiner_als_Pkt2 für 3 Fälle eine 1 ergibt und für einen Fall eine 0. 1 bedeutet True, also wahr. Die Aussage dass die Punktzahl_1 kleiner ist als Punktzahl_2 ist also wahr. 0 bedeutet False, also falsch. Da bei Fall 2 (Bärbel) der Wert von Punktzahl_1 (8) größer als der von Punktzahl_2 (7) ist, ist die Aussage das Punktzahl_1 kleiner ist als Punktzahl_2 für diesen Fall falsch.
Das Grundprinzip ist klar. Deshalb können wir uns als nächster Stufe einem möglichen Anwendungsfall widmen. Ein Anwendungsfall ist z. B. eine vorläufige Hypothesenprüfung.
Eine einfache Hypothese könnte lauten:
Unter der Annahme neurowissenschaftlicher Erkenntnisse (NameEinesAutors, Datum)
ist zu vermuten, dass bereits einmalige Übung bei Basketballwürfen eine Verbesserung der Trefferquote
bewirkt.
Wenn die Hypothese stimmt, dann müsste die Punktzahl einer zweiten Wurfserie höher sein, als die Punktzahl der ersten Wurfserie. Im Fall einer wissenschaftlichen Arbeit auf Hochschulniveau reicht dieses Testverfahren nicht aus. Da müssen wir statistisch anerkannte Verfahren nutzen, um Zufall auszuschließen und Lehrer/Dozenten/Verlage/... zufriedenzustellen. Einige der anerkannten Verfahren werden in den folgenden Artikeln besprochen.
Hier im Bild prüfen wir ob der Trainingseffekt gegeben ist. Weil wir mit kleinen Effekten nicht zufrieden sind, möchten wir dass uns nur Ergebnisse als wahr angezeigt werden, wo eine Verbesserung von 50% gegeben ist. Das ist ein Beispiel, häufig sind wenige Prozent bereits wertvoll.
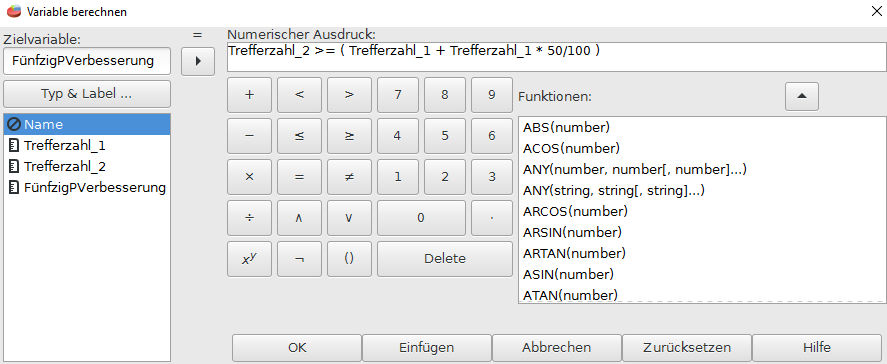
Wir geben die logische Formel in PSPP ein, die folgendes ausdrückt: Wenn die Trefferzahl_2 größer ist als Trefferzahl_1 (100%) + weitere 50%, dann ist die Aussage wahr (1).
Falls ihr euch was die Formel angeht nicht sicher seid, öffnet ein neues PSPP Dokument und testet eure Formel dort. Erstellt ein paar Beispielfälle und prüft, ob eure logische Formel in den richtigen Fällen falsch bzw. wahr ist. Wenn die Formel richtig ist, öffnet das Variablen Berechnen Fenster nocheinmal. Dort steht die jeweils letzte eingegebene Formel, kopiert sie und fügt sie in eurem Hauptdokument wieder ein.
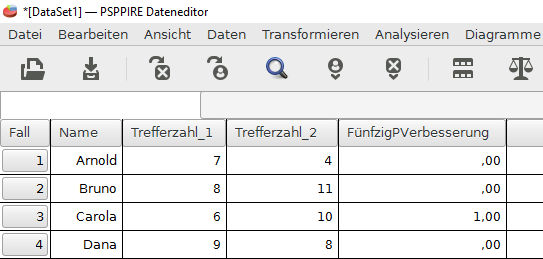
Das Ergebnis zeigt, dass eine Verbesserung um 50% nur in einem Fall auftritt. Nur Carola konnte eine 50% Verbesserung erreichen.
Letzendlich ist dies ein fiktives Beispiel, und 50% sind nur ein Wert, den wir als willkürliche Schwelle gesetzt haben. Wie bereits erwähnt, der Wert ist wahnwitzig groß. Wissenschaftler operieren mit Testverfahren, die eine statistische Signifikanz messen, dabei geht es u.A. um die Verteilung der Werte. Die Signifikanz kann auch bei kleinen Unterschieden gegeben sein.
Nächster Artikel: Skripte benutzen
