Test auf Normalverteilung
| Zurück zum Inhaltsverzeichnis |
| 0 - Testauswahl |
| 1 - Durchführung KS-Test |
Um den KS-Test für eine einzelne Stichprobe in PSPP auszuführen klicken wir im Menü auf Analysieren -> Nicht parametrische Tests -> 1 Sample KS-Test. Mit dem Test lässt sich prüfen, ob ein Merkmal in einer Stichprobe normalverteilt ist.
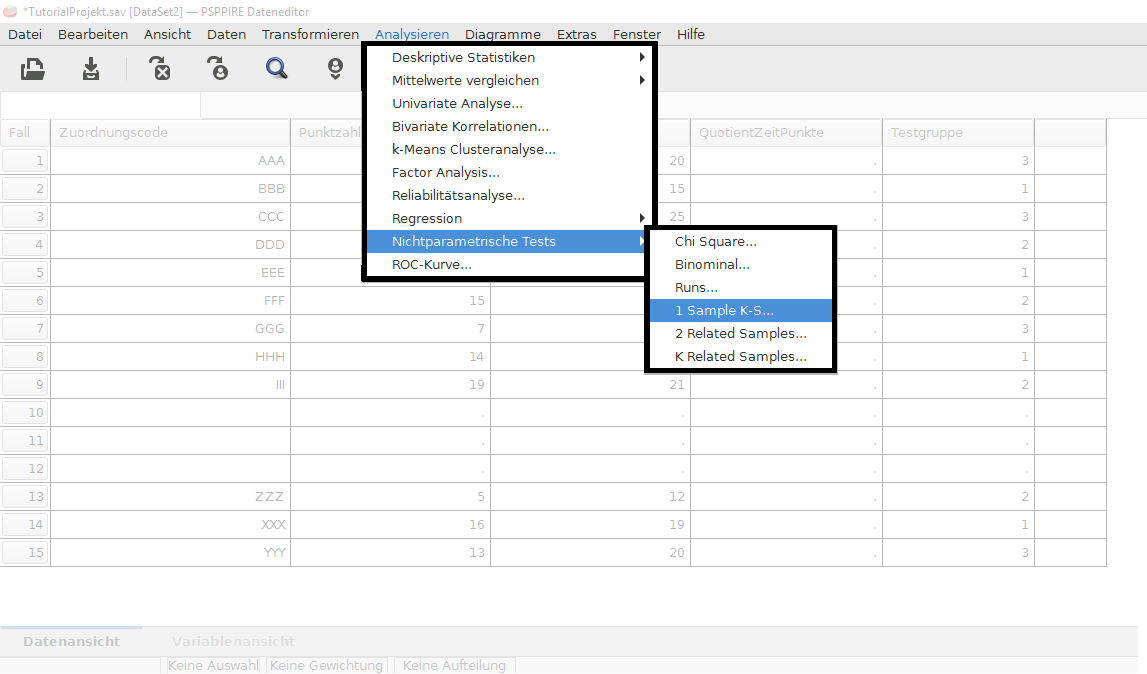
Das Menü zum KS-Test öffnet sich. Da der KS-Test verschiedene Anwendungsgebiete hat, müssen wir die Auswahlbox Normalverteilung aktivieren. Dann wählen wir die Variable aus, welche wir auf eine Normalverteilung überprüfen wollen. Im Beispielbild unten sehen wir am Verbotsschild-Icon, dass String-Variablen (Texte) nicht auf Normalverteilung geprüft werden können. Alle anderen Variablen können per Klick auf den Pfeil als Testvariable ausgewählt werden.
Es können auch mehrere Testvariablen ausgewählt werden. Diese werden einzeln mit dem KS-Test geprüft und in einer Tabelle in unterschiedlichen Spalten aufgelistet.
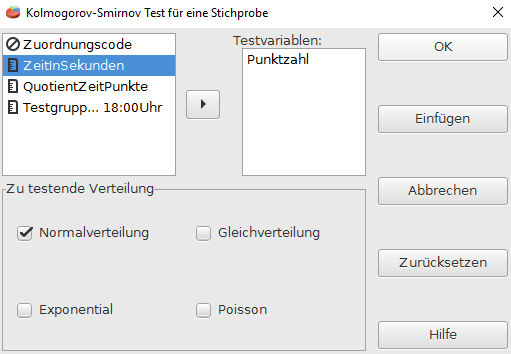
Das Ergebnis des Test finden wir im PSPP Ausgabefenster. Im Bild unten sind die Werte grün markiert, die wir für die Intepretation des KS-Test benötigen.
Bevor es losgeht. Was sind unsere Hypothesen die wir mit dem KS-Test prüfen? Die H0 Hypothese ist: Die vorliegenden Daten weisen eine Normalverteilung auf. Die H1 Alternativhypothese ist: Die vorliegenden Daten weichen von einer Normalverteilung ab.
Um den Test aus PSPP auszuwerten müssen wir den kritischen Wert mit Referenzdaten vergleichen. Im Internet finden sich viele Quellen, am besten ist jedoch immer ein Statistikbuch. Die Werte die hier aufgelistet sind, entsprechen einem Wert von α=0,05. α bezeichnet das Signifikanzniveau, auf das getestet wird. Wenn ihr euch mit Signifikanz nicht auskennt, schlagt den Begriff nach, denn ihr kommt beim wissenschaftlichen Arbeiten nicht drumherum.
Der Kritische Wert (absolut) 0,10 wird mit den Werten der Referenztabelle (unten) verglichen. Da wir 12 Datensätze geprüft haben, müssen wir in der Tabelle unter n=12 nachschlagen, dort steht der Wert 0,375. Der Wert in der Tabelle (0,375) bezeichnet einen Grenzwert, ab dessen Überschreitung die H1 Hypothese (Abweichung von der Normalverteilung) abgelehnt werden muss. In unserem Fall liegt der Wert 0,10 unter dem Grenzwert 0,375. Deshalb können wir die H1 Hypothese nicht annehmen und die H0 Hypothese nicht ablehnen. Es ist etwas verwirrend, aber der KS-Test erlaubt nicht die Bestätigung der H0 Hypothese. Er erlaubt nur die Folgerung, dass wir die H1-Hypothese (Abweichung von einer Normalverteilung) nicht annehmen können. Der Grund für die Vorsicht ist, dass wir den Fehler zweiter Art (auch β-Fehler) nicht kennen.
Ein weiterer Wert ist hier als asymptotische Signifikanz bezeichnet. In unserem Fall wurde mit Der Signifikanz von α = 0,05 getestet. Ist der Wert der asymptotischen Signifikanz größer als der Wert von &alpha, so können wir die H0-Hypothese nicht ablehnen. Ist der Wert der asymptotischen Signifikanz hingegen kleiner als &alpha, so könnten wir nur mit 5% Wahrscheinlichkeit annehmen, dass die Daten eine Normalverteilung aufweisen. Hier im Beispiel liegt eine asymptotische Signifikanz von 1 vor. Unter dieser Voraussetzung können wir die Annahme der H0-Hypothese nicht ablehnen.
Wir können den Wert von α auch anders wählen. Z.B. als α = 0,1. Dies tun wir, wenn wir strikter testen wollen. Je enger wir die Grenzen setzen, desto aussagekräftiger sind die Testergebnisse. Bei einem asymptotischen Signifikanzwert von 0,09 würden wir im Fall von α = 0,1 die H0-Hypothese ablehnen. Bei α = 0,05 und einem asymptotischen Wert von 0,09 können wir die H0-Hypothese nicht ablehnen.
Falsifizierung
Wir sagen nie: Hier liegt eine Normalverteilung vor,
sondern wir können nicht ablehnen dass eine Normalverteilung vorliegt.
Es wäre natürlich schöner eine klare eindeutige Aussage zu treffen,
aber die Wissenschaft möchte ein wahres Ergebnis.
Das Prinzip der Falsifizierung ist eine Grundlage von Wissenschaft,
die wir auch in der Aussagenlogik wiederfinden. Statistiker kennen Wege der Verifizierung
von Hypothesen, wenn die Fehlerwahrscheinlichkeiten bekannt sind.
Philosophen (Logik) wollen jedoch nicht über wahrscheinliche sondern definitive Ergebnisse reden.
Sie nehmen immer an, dass unser Wissen fehlerhaft sein kann.
Die Aussage "Alle Schwäne sind weiss" wird mit dem Fund eines schwarzen Schwans abgelehnt (falsifiziert).
Die Aussage "Einige Schwäne sind weiß" ist hingegen niemals abzulehnen,
selbst wenn wir nur schwarze Schwäne kennen.
Denn vielleicht lebt ja in einem abgelegenen Waldsee, der uns unbekannt ist, eine Gruppe weißer Schwäne.
Solange wir nicht den Fehler beherrschen können, durch Allwissenheit (Logik) oder Kenntnis des Fehlers (Statistik)
solange müssen wir falsifizieren und nicht verifizieren.
Tabelle mit kritischen Werten. Quelle: faes.de
| n | kritischer Wert (α = 0,05) |
|---|---|
| 3 | 0,708 |
| 4 | 0,624 |
| 5 | 0,563 |
| 6 | 0,519 |
| 7 | 0,483 |
| 8 | 0,454 |
| 9 | 0,43 |
| 10 | 0,409 |
| 11 | 0,391 |
| 12 | 0,375 |
| 13 | 0,361 |
| 14 | 0,349 |
| 15 | 0,338 |
| 16 | 0,327 |
| 17 | 0,318 |
| 18 | 0,309 |
| 19 | 0,301 |
| 20 | 0,294 |
| 21 | 0,287 |
| 22 | 0,281 |
| 23 | 0,275 |
| 24 | 0,269 |
| 25 | 0,264 |
| 26 | 0,259 |
| 27 | 0,254 |
| 28 | 0,25 |
| 29 | 0,246 |
| 30 | 0,242 |
| 31 | 0,238 |
| 32 | 0,234 |
| 33 | 0,231 |
| 34 | 0,227 |
| 35 | 0,224 |
In einigen Tabellen finden sich auch Werte bis 40. Wenn die Werte größer als n=40 sind, müssen die Werte mit einer Formel berechnet werden: Formel auf mard.wiwi.hu-berlin.de
Wenn ihr den KS-Test mit Liliefors-Korrektur analysieren wollt, braucht ihr die Liliefors-Tabelle. Die findet sich u.A. bei folgendem Anbieter kommerzieller Dienste: real-statistics.com
Nächster Artikel: Test auf Zusammenhang (Korrelation)
