Korrelation bestimmen
| Zurück zum Inhaltsverzeichnis |
| 0 - Testverfahren Zusammenhang |
| 1 - Bivariate Korrelation |
| 2 - Multiple Regression |
Wenn wir eine Korrelation zwischen zwei Variablen pr�fen, nennt man dies eine Bivariate Korrelation. Im Men� klicken wir auf Analysieren -> Bivariate Korrelationen
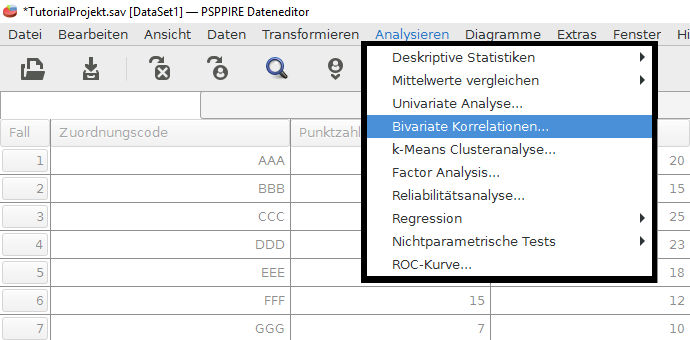
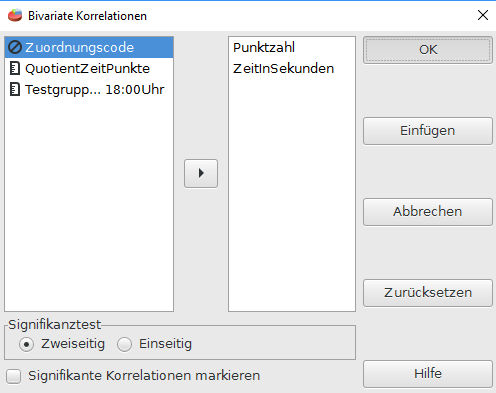
Im sich �ffnenden Fenster w�hlen wir Variablen aus, die wir miteinander vergleichen wollen. Wir k�nnen auch mehr als zwei Variablen ausw�hlen. In diesem Fall werden die Variablen in einer Tabelle gegen�bergestellt und jede mit jeder anderen verglichen. Es handelt sich dann nicht um eine Multiple Korrelation, sondern nur um eine Bivariate Korrelation, bzw. genauer gesagt um mehrere Bivariate Korrelationen nacheinander.
Mit dem Pfeil f�gen wir die Variablen von rechts nach links hinzu. Ganz wichtig ist, dass ihr unter dem Men�punkt Signifikanz die richtige Option ausw�hlt. Da alle Korrelationen ungerichtet sind, w�hlen wir die Option zweiseitig.
Erkl�rung zu gerichtet/ungerichtet
Bei ungerichteten Hypothesen wird das zweiseitige Testverfahren gew�hlt.
Bei gerichteten Hypothesen wird das einseitige Testverfahren gew�hlt.
Die Regression gegen�ber der Korrelation z. B. ist immer gerichtet.
Ungerichtet meint, dass die Variablen gleichberechtigt sind.
Gerichtet meint, eine Variable bestimmt eine andere Variable,
Z.B. ist Torsch�sse (Fu�ball) die unabh�ngige Variable und erzielte Tore die abh�ngige Variable.
Umgekehrt ergibt das auch keinen Sinn, denn das bereits erzielte Tor f�hrt nicht dazu,
dass jemand aufs Tor schiesst.
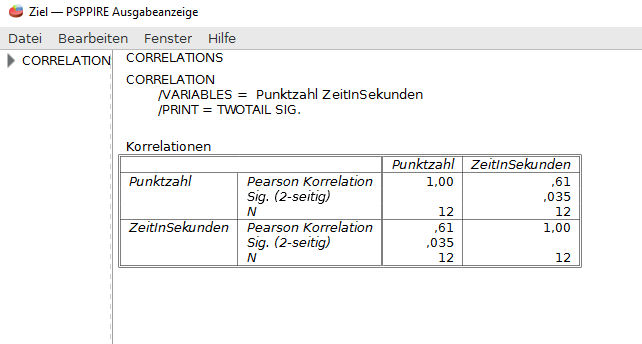
Nach dem Klick auf OK erhalten wir im Ausgabefenster von PSPP unser Ergebnis. Wir sehen dass unsere Stichprobe N=12 Datens�tze aufweist. Der Korrellationskoeffizient zeigt uns 0,61 an. Es handelt sich um eine positive Korrelation. Wir schauen in unseren Referenzwerten nach und sehen dort, 0,61 ist als starke Korrelation zu interpretieren. Also scheint ein starker Zusammenhang zwischen den Werten zu bestehen. So sollte es auch sein, denn ich habe die Werte extra ungef�hr so f�r das Beispiel eingetippt. Wer mehr Zeit brauchte hat mehr Punkte erhalten.
Allerdings habe ich kein festes System bei der Eingabe der Werte genutzt, weshalb die Werte etwas zuf�llig erscheinen. Dies zeigt sich auch am Signifikanzwert. 0,35 erreicht kein Signifikanzkriterium. Das schw�chste Signifikanznivea liegt bei 0,05. Bei dem Wert von 0,35 ist von einer gewissen Zuf�lligkeit auszugehen.
Da das vorherige Ergebnis zuf�llig wirkte, habe ich f�r das Beispiel die Werte erneut nach einem festen System eingegeben. Die Werte der ersten Variablen wurde f�r die zweite Variable einfach verdoppelt, so dass ein Anstieg von Variable 1 auch zum Anstieg von Variable 2 f�hrte. Anschlie�end wurden noch ein paar pseudo-nat�rliche Abweichungen hinzugef�gt. Das Ergebnis ist eine Korrelation von 0,94, also ein sehr starker Zusammenhang.
Und diesmal ist auch die Signifikanz auf h�chstem Niveau gegeben. Der Wert 0 sagt uns: Dieses Ergebnis ist statistisch gesehen kein Zufall! Wie wahr ;) Die Grenzwerte 1 und 0 sind auf nat�rlichem Wege bei gro�en Stichproben nur theoretisch zu erreichen, bei kleinen Stichproben kann der Zufall aushelfen.

Nächste Seite: Multiple Regression.
